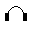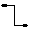O tom, že vlastnosti poslechového prostoru mají velmi podstatný vliv na kvalitu poslechu jste se už jistě mnohdy a mnohde dočetli či doslechli. Hlavně v časopisech určených pro hudebníky se vyskytují zmínky o tom, jak to chodí v nahrávacích studiích či koncertních síních, a možná by se našel i nějaký náznak na téma, co podniknout doma, aby nám ruku v ruce s hifi zařízením „hifoval“ i obývák či jiný prostor k poslechu využívaný. A my se na téma „Domácí poslechový prostor a co s ním“ podíváme trochu podrobněji.
Základní pojmy
Akustika je odvětví fyziky, které se zabývá zvukem a vším co s ním souvisí, především pak šířením zvukových vln (a vším s ním spojeným). Zvukové vlny jsou zjednodušeně řečeno vlny, které jsou přenášeny pružnou deformací prostředí, ve kterém se šíří. Tady stojí za to podotknout, že vlny na vodě, které se dosti často používají jako názorná analogie pro výklad šíření zvuku, jsou něco naprosto jiného – při šíření vln na vodě totiž k žádné pružné deformaci prostředí (tedy vody) nedochází. Deformace mohou být různého druhu. Nejsložitější je to v pevném (tuhém) prostředí, to však má pro nás naštěstí význam pouze okrajový. Nás bude zajímat především šíření zvuku ve vzduchu, což je prostředí plynné. Z hlediska šíření zvuku i jiných fyzikálních hledisek jsou si velmi podobné prostředí plynné a kapalné (plyny a kapaliny se z tohoto důvodu zahrnují pod společný pojem tekutiny, takže můžeme hovořit obecně o prostředí tekutém). Pro tekuté prostředí je charakteristické to, že v prvním přiblížení (speciálně při zanedbání viskozity) v něm nemohou existovat ohybové a smykové (střihové) deformace, tekuté prostředí a tedy i vzduch se může deformovat pouze objemově (akustiku kapalin čili hydroakustiku prozatím ponecháme stranou).
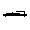
Nejjednodušším příkladem objemové deformace vzduchu je jeho stlačování (např. pístem) v uzavřené nádobě (např. válci). Schématicky je to znázorněno na obr. 1:

Vzduch stejně jakýkoli jiný plyn se skládá z molekul. Pokud by molekuly plynu zůstávaly stále na stejném místě, pak by se při pohybu pístu ve válci molekuly v blízkosti pístu „shrnuly“ do části prostoru poblíže pístu podobně jako třebas zrnka písku a dál by se nic nedělo. Molekuly jsou však v neustálém pohybu, poletují sem tam, srážejí se, odrážejí se od sebe a předávají si energii a hybnost. Jejich celková energie v nějakém konkrétním objemu se nazývá vnitřní energie a navenek se projevuje tím, že plyn má určitou teplotu. Molekuly plynu uzavřeného v nádobě narážejí také na stěny nádoby a odrážejí se od nich, což se projevuje jako tlak plynu na stěny nádoby.
Tlak plynu je tím větší, čím rychleji se molekuly pohybují, neboli čím vyšší teplotu plyn má. Je také tím větší, čím více molekul je obsaženo v daném objemu , neboli čím vyšší je hustota plynu. Avšak pozor! Touto hustotou se rozumí počet molekul na jednotku objemu plynu a nemá to nic společného s hustotou ve smyslu hmotnosti na jednotku objemu, která se udává např. u pevných látek. Kupříkladu molekula kyslíku je šestnáctkrát těžší než molekula vodíku, jestliže však do objemu jednoho litru napustíme jeden trilion molekul kyslíku (1018, 1 000 000 000 000 000 000 molekul), což je mimochodem poměrně málo, pak v tomto objemu bude stejný tlak, jako kdybychom do něj napustili jeden trilion molekul vodíku, i když celková hmotnost v případě vodíku bude šestnáctkrát menší (ten tlak bude přibližně 0,000037 atmosféry).
Vzájemný pohyb molekul a jejich srážení způsobí, že když v nějaké části objemu plynu dojde ke změně hustoty, např. pohybem pístu, tato změna se velmi rychle rozšíří do celého prostoru, který plyn zaujímá, a vytvoří se nový rovnovážný stav, ve kterém jsou molekuly opět rozptýleny víceméně rovnoměrně, jen jejich průměrná vzdálenost je jiná. Při zmenšení objemu stlačením pístu se plyn zhustí a jeho tlak v důsledku toho stoupne. Kromě toho obvykle také stoupne jeho teplota. To se stane tehdy, jestliže plyn je v uzavřeném objemu tepelně izolován. Na stlačení plynu totiž musíme vynaložit určitou energii (pro pohnutí pístem musíme působit nějakou silou po nějaké dráze a konáme tudíž práci) a tato energie se v konečném výsledku přenese na plyn, kterému stoupne vnitřní energie a tím pádem i teplota. Souvislost mezi objemem, tlakem a teplotou plynu popisuje tzv. stavová rovnice plynu, ale tou už se zabývat nebudeme, ono té fyziky už i tak bylo dost.
Představme si nyní, že máme píst ve volném prostoru, tedy v neomezeném objemu. Co se může stát, bude nám ilustrovat obr. 2.

Píst je obklopen plynným prostředím, složeným z molekul, a toto prostředí má v klidovém stavu jistý rovnovážný tlak. Jestliže se píst pohne z místa v směru kolmém na jeho plochu, dojde v blízkosti jedné strany ke krátkodobému nárůstu hustoty (zhuštění) a na opačné straně k poklesu (zředění) prostředí obklopujícího píst. U části molekul také dojde ke změně rychlosti ve směru pohybu pístu. Tuto změnu molekuly předávají prostřednictvím nárazů dalším a dalším molekulám a oblasti zředění a zhuštění se budou pohybovat směrem od pístu. Takto vznikne pohybem pístu vybuzená zvuková vlna (vlastně dvě zvukové vlny). V oblastech zředění a zhuštění dojde ke změně tlaku plynu oproti rovnovážnému stavu. Velikost této odchylky se nazývá akustický tlak. Nejnižší velikost akustického tlaku, kterou je lidský sluch schopen zaregistrovat jako zvuk, je přibližně 2.10-5 Pa (atmosférický tlak je přibližně 100 000 Pa).
Trochu složitější je to s rychlostí pohybu molekul. Každá molekula se pohybuje jistou rychlostí, u plynu v klidovém stavu jsou však všechny směry pohybu stejně pravděpodobné a výsledná rychlost pohybu plynu jako celku je nulová. Pokud plynem prochází zvuková vlna, vzniká v oblasti vlny odchylka rychlosti jednotlivých molekul od rovnovážného stavu, takže průměrná hodnota vektorů rychlosti molekul již není nulová, nýbrž udává akustickou rychlost. Rychlost pohybu zvukové vlny jako celku prostředím pak je pro dané prostředí rychlost zvuku, která obecně závisí na vlastnostech prostředí a ve vzduchu za běžných podmínek činí přibližně 343 m/s.
Vektor je veličina, která je charakterizována velikostí a směrem. Takovou veličinou je např. právě rychlost. Popisujeme-li rychlosti pohybu jednotlivých molekul jako vektory, pak u plynu v klidu je jejich průměrná rychlost, daná jako aritmetický průměr vektorů rychlostí všech molekul, rovna nule – tedy nulovému vektoru. Veličina, která je určena pouze velikostí, se nazývá skalár. Typický skalár je např. teplota. S teplotou souvisí vnitřní energie plynu. Souvisí také s rychlostí molekul, není však dána sčítáním vektorových hodnot, nýbrž druhých mocnin velikostí vektorů rychlosti jednotlivých molekul bez ohledu na směr a není to tedy vektor, nýbrž také skalár. Průměrná velikost rychlosti tepelného pohybu molekul vzduchu za pokojových podmínek je přibližně 470 m/s.
Zvukovou vlnu je samozřejmě možné vybudit i jinými způsoby než pohybem nějakého konkrétního pístu. Jako píst může například fungovat část rezonanční desky hudebního nástroje. Zvuková vlna se vybudí také když se někde v plynném prostředí prudce změní teplota – například při elektrickém výboji. Anebo se může stát, že z nějakého důvodu dojde k lokálnímu zvýšení množství molekul plynu – třebas při explozi, výstřelu apod. Nejjednodušším a v jistém smyslu mezním případem je situace, kdy oblast vzniku zvukové vlny je bodová a zvuková vlna se od ní šíří všemi směry. Pokud prostředí, v němž se vlna šíří, je homogenní, pak místa, do kterých vlna dospěje za určitý čas, tvoří kulové plochy (vlnoplochy) a můžeme hovořit o zvukových paprscích, což jsou polopřímky s počátkem v bodě zdroje, kolmé k vlnoplochám.
Zvukové události, kterými jsme si zatím demonstrovali základní akustické jevy, byly jednorázové – třeskne výstřel, prostorem kromě kulky proletí zvuková vlna a dál se nic neděje (tedy téměř). Zvuky však bývají zpravidla trvalejšího charakteru a zvláštní postavení mají ty, které se pravidelně opakují. Fyzikálně se to vyjádří tak, že si zvuk popíšeme jeho časovým průběhem, tedy funkcí, která udává závislost akustického tlaku na čase v nějakém bodě prostoru, kterým zvuk prochází. Úplný popis zvukového dění bychom dostali, kdybychom dokázali zkonstruovat funkci, která by časový průběh akustického tlaku popisovala v celém prostoru. Nezávislými proměnnými takové funkce by byly tři prostorové souřadnice a čas, závisle proměnnou pak akustický tlak. Prozatím však vystačíme jen s akustickým tlakem a časem. Jestliže lze najít nějaký časový úsek (interval), po jehož uplynutí se časový průběh přesně opakuje, po zopakování tohoto intervalu se opět opakuje ... a tak dále znovu a znovu, nazýváme takový časový průběh periodickým, „opakovací“ interval je perioda a počet period za jednotku času je frekvence. A ještě jedna důležitá veličina; vzdálenost, kterou zvuková vlna urazí za dobu jedné periody, se nazývá vlnová délka. Délka periody má rozměr času, takže nejčastěji ji měříme v sekundách (případně v metrických zlomcích – milisekunda, mikrosekunda...). Frekvence má rozměr převrácené hodnoty času a její jednotkou je hertz [Hz], což je frekvence odpovídající jedné periodě za sekundu; samozřejmě se používají i násobky – kilohertz [kHz], megahertz [MHz] atd. Lidský sluch je schopen vnímat zvuky o frekvencích v rozmezí přibližně 20 Hz až 20 kHz (s postupujícím věkem se horní hranice snižuje, např. autor tohoto článku slyší zvuky o frekvenci nejvýše přibližně 14,5 kHz). Pro obvyklé hodnoty rychlosti zvuku ve vzduchu tomu odpovídá rozpětí vlnových délek zhruba 17 m až 17 mm.
Akustika a prostor
Prostorovou akustikou se rozumí ta část akustiky, která se zabývá zvukovým děním uvnitř prostoru, přičemž zpravidla neřeší problémy související s tím, kde se zvuk v prostoru vzal. Zvuk se může vytvořit uvnitř zkoumaného prostoru např. hrou na hudební nástroj (s tím související jevy patří do oboru hudební akustiky) nebo činností nějakého ozvučovacího zařízení (to je doména elektroakustiky), případně do něj může proniknout z vnějšího světa, čímž se zabývá především stavební akustika. Pro prostorovou akustiku je však podstatné to, co se v prostoru děje, když už v něm zvuk je. Základní problém prostorové akustiky se vlastně dá vyjádřit mírně modifikovaným zněním klasického přísloví - jak se z prostoru (anebo v prostoru) ozývá, když se do něj volá.
Prostorová akustika tedy zkoumá osud zvukového signálu v prostoru, ohraničeném (případně přímo uzavřeném) překážkami, jakými jsou například stěny. Zajímá se o to, kudy se zvukový signál pohybuje a co se s ním přitom děje. Při popisu tohoto dění se vychází z představy zvukového paprsku. Zvuk je sice ve své podstatě vlnění, jak jsme si však již řekli, zvukový signál se v homogenním prostředí od svého zdroje šíří víceméně přímočaře, takže využití analogie s paprskem třeba světelným je docela namístě. A pokud je zapotřebí pracovat s vlnovou představou, používá se pojmu vlnoplochy. Zvukové vlny, paprsky a vlnoplochy si tedy poletují v prostoru a prostorová akustika v první řadě potřebuje vědět, co se s nimi stane, když do něčeho narazí. Tedy, co to vlastně znamená - narazí. Zatím jsme si popisovali, co se děje, když se zvuková vlna šíří vzduchem. Při takovém šíření narážejí do sebe navzájem molekuly plynů tvořících vzduch . Něco jiného se bude dít, když na předpokládané dráze vlny najednou přestane být vzduch a začne tam být něco jiného, třeba zeď, obecně tedy pevná překážka. Molekuly plynu začnou narážet do molekul materiálu tvořícího překážku a co se v takovém případě stane, je velice složité a na přesný popis velice náročné dění, jehož konkrétní podoba závisí především na tom, jaké vlastnosti překážka má. Pro potřeby prostorové akustiky není třeba znát, co se děje s jednotlivými molekulami, postačí, když toto dění popíšeme s pomocí paprsků nebo vlnoploch.
Schématicky je toto dění naznačeno na obr. 3.

Schéma naznačuje tyto základní jevy:
1. Při dopadu paprsku na rozhraní se část energie odrazí, zbytek vnikne do překážky
2. Zbývající energie se šíří materiálem překážky v podobě zvukových vln v pevném prostředí a při tomto šíření se část zvukové energie mění na teplo, takže zvukové vlny se tlumí
3. Část zvukové energie šířící se překážkou vystoupí na druhé straně překážky (resp. přepážky), část se prostřednictvím odrazů uvnitř překážky vrátí – samozřejmě dále utlumená – zpět do té části vzduchového prostředí, odkud přišel primární paprsek.
Takto detailní rozbor zpravidla pro prostorovou akustiku není nutný, obvykle vystačíme s tím, že při dopadu paprsku na materiálové rozhraní se prostě odrazí jen jistá část energie. Poměr množství odražené energie k dopadající je popsán činitelem odrazivosti, v prostorové akustice však zpravidla pracujeme s činitelem pohltivosti, který je označován řeckým písmenem α a rovná se doplňku činitele odrazivosti do jedné (jedna mínus činitel odrazivosti). Jak vyplývá ze schématu na obr. 3, udává sice činitel pohltivosti ztráty energie při odrazu, ve skutečnosti ale nemusí jít nutně o pohlcování v pravém slova smyslu, poněvadž část energie, která se neodrazila, může být např. vyzářena někam jinam. Používání termínu „činitel pohltivosti“ je však natolik vžité, že nemá smysl vymýšlet si pro popis „energetické bilance“ odrazu něco jiného.
Při dopadu zvukové vlny (nebo paprsku, je-li libo) na materiálové rozhraní se odrazí tím větší poměrná část energie, čím více se mechanické vlastnosti odrážejícího materiálu liší od vlastností vzduchu. Jde hlavně o hustotu resp. hutnost a tuhost (hustotou v tomto případě rozumíme to, co se dříve nazývalo specifická váha nebo specifická hmotnost). V běžném jazyce to lze vyjádřit tak, že čím je materiál tvrdší, těžší a kompaktnější, tím lépe odráží zvuk. Ta kompaktnost je velmi podstatná, existují totiž materiály, které jsou sice tvrdé a těžké, avšak pórovité a díky pórovitosti podstatně více zvuku pohltí nežli odrazí. K tomu se vrátíme později. A je tady ještě jedna důležitá okolnost – překážka zvuk odráží pouze v případě, že její rozměry jsou srovnatelné s vlnovou délkou dopadajícího zvuku anebo jsou větší. Dá se říci, že vlna o dlouhé vlnové délce „nevidí“ malou překážku a při svém šíření ji jaksi „ze všech stran obejde či obteče“. Hranice mezi tím, co je akusticky malé a co velké, přitom není ostrá – je to spíše jakési pásmo někde mezi čtvrtinou vlnové délky a vlnovou délkou. Fyzikálně se to popisuje velmi složitě, takže se raději spolehnu na představivost a intuici čtenářů.
Něco podobného funguje i v případě samotného odrazu ve vztahu k hladkosti či nerovnosti povrchu. Pokud je odrazná plocha rovná a hladká, je odraz zrcadlový; pokud je zakřivená nebo nerovná, dochází k rozptylu zvuku, přičemž o míře zakřivenosti či hrbolatosti v souvislosti s rozměry nerovností platí opět to, co se táhne jako červená nit celou akustikou - co je menší než zhruba čtvrtina vlnové délky, to zvuková vlna „nevidí“, takže stěna je pro ni hladká, jestliže nerovnosti na ní jsou menší než ona čtvrtvlna.
Představme si nyní, že máme nějaký uzavřený prostor a začneme do něj „napouštět zvuk“, třebas tak, že uvedeme do provozu ozvučovací zařízení, začneme zpívat nebo pracovat se sbíječkou. Do prostoru přichází zvuková energie, vlnoplochy a paprsky poletují sem tam, rozkmitávají molekuly vzduchu a odrážejí se od stěn či jiných překážek v prostoru se vyskytujících. Celkové množství energie zvukového pole postupně narůstá, při každém odrazu od překážky však dojde ke ztrátě energie, která je tím větší, čím větší je energie na překážku dopadající. Po jisté době se tak ustálí rovnovážný stav, při kterém množství energie do prostoru přiváděné je stejné jako množství energie unikající z prostoru v důsledku ztrát. Akustické pole tvořené odraženým zvukem, tedy soustavou vlnoploch nebo paprsků, které na své pouti absolvovaly alespoň jeden odraz, se nazývá pole odražených vln. Někdy se ne zcela přesně používá také název „difúzní pole“ Ten vychází z idealizované představy, že v ustáleném stavu je hustota energie v prostoru rozdělena rovnoměrně (pole je homogenní) a tok energie v kterémkoli bodě a kterémkoli směru je stále stejný (pole je izotropní). Tato představa nikdy nemůže přesně odpovídat realitě, je však užitečná pro některé teoretické úvahy. Pro doplnění, pole tvořené přiváděným zvukem, který ještě žádným odrazem neutrpěl, se nazývá přímé pole.
Z hlediska prostorové akustiky je důležité, co se stane, když se množství zvukové energie do prostoru přiváděné změní (jevy tohoto druhu jsou vlastně v prostorové akustice prvořadým předmětem zkoumání). Krajním případem takové změny je úplné přerušení přívodu energie. Je jasné, že v tomto případě z prostoru velmi rychle zmizí přímé pole. Pole odražených vln však ještě nějakou dobu přetrvává, a to proto, že z prostoru může vymizet jedině ztrátami při odrazech od překážek, které prostor obklopují popř. vyplňují. A k těmto překážkám se nejdříve musí nějak dostat, což vzhledem ke konečnosti rychlosti šíření trvá nějakou dobu. Důsledkem je, že množství energie v prostoru po přerušení přívodu energie bude klesat, a to víceméně pozvolna (tj. nezmizí ihned). Prostorová akustika zkoumá, jak konkrétně tento pokles bude vypadat a jak bude jeho charakter záviset na takových vlastnostech prostoru, jakými jsou jeho rozměry, vlastnosti materiálů odrazných ploch a jejich geometrické uspořádání. Jev spočívající v pozvolném poklesu množství zvukové energie po přerušení jejího přívodu do prostoru se nazývá dozvuk. Tímto názvem se obvykle označuje také samotný zvuk vytrácejícího se akustického pole, neboli to, co slyšíme poté, co zmizel zdroj zvuku. Pojem „dozvuk“ je asi známý každému, kdo k akustice nebo elektroakustice aspoň přičichl, a i ten, kdo nezná přesnou definici, ví, co to v praxi znamená.
Jedním z hlavních praktických úkolů prostorové akustiky je optimalizace dozvuku tak, aby jeho charakter byl v souladu s tím, k čemu má být prostor používán. Je přitom důležité si uvědomit, že dozvukové pole se začne vytvářet ihned poté, co do prostoru začneme zvukový signál přivádět. Přímý (primární) zvuk se na intenzitě sluchového vjemu podílí zpravidla výrazně větší měrou než dozvuk. Přítomnost dozvuku souběžně s přímým zvukem však přesto má na kvalitu sluchového vjemu významný vliv, například mění barvu vnímaného zvuku a díky schopnostem sluchového orgánu ovlivňuje do jisté míry orientaci v prostoru. Podle charakteru doznívání dokážeme na základě zkušenosti alespoň přibližně odhadnout, v jakém prostoru se právě nacházíme. Rozlišíme jeskyni od koupelny, kostel od ložnice a poznáme, kdy jsme na volném prostranství, kde vcelku žádný dozvuk není.
Optimalizace dozvuku znamená „ani moc, ani málo“. Například pobyt v uzavřeném prostoru bez dozvuku (suchém, mrtvém) působí nepříjemně až depresivně. Na druhé straně pokud má poslechový prostor dozvuku příliš mnoho, dochází např. při poslechu hudby k deformaci sluchového vjemu oproti tvůrčímu záměru, při poslechu mluveného slova k ztrátě srozumitelnosti a tak dále. Dozvuk může ovlivnit (v krajním případě i znemožnit) lokalizaci zdroje primárního zvuku v prostoru (tedy odhadu polohy zdroje zvuku prostřednictvím sluchu) a ještě větší vliv může mít na lokalizaci zdánlivého zdroje zvuku při stereofonní reprodukci – v takovém případě jde zpravidla o změnu přesnosti lokalizaci, nikoli přímo o změnu polohy. Dozvuk je tedy věc velmi důležitá a jeho podrobnější zkoumání nezbytné.